En este curso, he realizado junto a mi alumnado de taller de matemáticas un triángulo de Sierpinski creado con latas de refresco. Lo primero, agradecer a mis alumnos su disposición e ilusión que pusieron en dicha tarea. Nota: esta idea la encontré en esta presentación. De Proyecto Sierpinski De entre los diferentes proyectos que les …
Categoría: Matemáticas
Ene 23
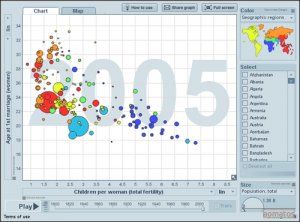
Gapminder, una visión del mundo basada en datos
Gapminder es una fundación sin fines de lucro con sede en Estocolmo. Tal y como se dicen ellos mismos, tratan de dar una visión del mundo basada en los hechos (for a fact-based world view) poniendo a nuestra disposición un método que nos haga más fácil entender los datos. Nos dotan, entre otras cosas, de una …
Jul 31
Recursos matemáticos para 1º ESO y mucho más
Hace unos días, una buena amiga a la que tengo un especial cariño, me comentó que iba a tener que impartir clases de matemáticas en 1º de la ESO (ella no es de mates) y le recomendé una serie de recursos. La mayoría son o bien libros interactivos o contienen unidades didácticas completas o excelentes …
Feb 14
Inspiración matemática
En los siguientes artículos de este blog, ya he puesto unos maravillosos vídeos creados por Cristóbal Vila de Etérea Studios: Geometría en los templos persas: Isfaban. Números en la naturaleza. En este artículo os invito a ver esta otra maravilla de Criśtobal titulada «Inspiration«, que tal y como dice, trata de imaginar como sería el escritorio …
Ago 10
Sistema Solar en 3D
En «Interactive 3D model of Solar System» podemos encontrar una fascinante herramienta para ver el Sistema Solar en tres dimensiones. Su funcionamiento es extremadamente sencillo, todo se hace a golpe de clic y las principales cosas que podemos hacer son: Ver la posición de los planetas y sus orbitas solares. Calcular la distancia de cualquiera …
May 22
Vídeo geométrico
Os dejo un bonito vídeo que muestra el transcurrir de dos puntos por la geometría en el plano: Espero que os guste.
Abr 29
Poesía y Pi
Imagen de BrittneyBush en Flickr [link] Esta es, y no lo es, una entrada al número , dos poesías os pongo, alguna relación más con él tendrán y más pistas no os puedo dar. Con la primera voy a empezar, espero que os guste no más: Soy y seré a todos definible, mi nombre tengo que daros, …
Abr 26
¿Más Sprite o Coca Cola? [Sol]
En una entrada anterior planteé este problema sacado del blog de Dan Meyer. Tras ver el siguiente vídeo había que responder que vaso contenía más bebida original, el de Sprite o el de Coca Cola. [WCYDWT] Coke v. Sprite from Dan Meyer on Vimeo. El resumen de las respuestas enviadas es: El problema era …