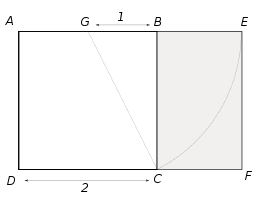
Mi blog de mates «MatemaTICzando la realidad» va poco a poco tomando cuerpo; mientras tanto, hay algunas entradas que las publico en ambos blogs (no sé si es la mejor opción). Por lo tanto, el clon de esta entrada en el otro blog lo tenéis aquí. Al empezar a ver las áreas de las principales …
Categoría: Geometría
May 22
Vídeo geométrico
Os dejo un bonito vídeo que muestra el transcurrir de dos puntos por la geometría en el plano: Espero que os guste.
Ene 02
Geometría en los templos persas: Isfahan
Y para empezar el año nada mejor que un hermoso vídeo titulado «Isfaban» creado por Etérea Studios de Cristóbal Vila. Si hay dos disciplinas fuertemente relacionadas, éstas son el arte y la geometría. En el vídeo podéis encontrar una bella simbiosis de ambas. Para los amantes del arte, el vídeo muestra la belleza del arte …
Dic 01
Proyecto Gauss
El ITE ha desarrollado el Proyecto Gauss con la finalidad de dar al profesorado items didácticos y applets (pequeñas aplicaciones) de Geogebra para cubrir los contenidos dematemáticas de 5º, 6º de primaria, 1º y 2º de la ESO. Para los que no sabéis lo que es un applet os pongo el que usan de cabecera …
Nov 22
Números en la naturaleza
Este es el primer artículo que escribo en este nuevo dominio (aomatos.com). No tenía muy claro con que tipo de artículo escribir al comenzar esta nueva andadura. Tras mucho meditarlo, he decidido orientarme hacia esa pasión que siempre he tenido y sigue entreteniéndome tanto como las TIC: las matemáticas. Alguna relación tenía que tener con las …