Jun 18
El otro dÃa llamé por teléfono a mi sobrino. Os pongo la conversación: – ¿Qué haces?– Aquà estoy, construyendo un triángulo de alturas 10, 20 y 30 cm. Pero no hay manera de que me salga.– Ya lo voy a pensar y te contesto. ¿Cual serÃa la contestación correcta?.
Jun 16
He visto este acertijo en Acertijos y mas cosas. No es un acertijo difÃcil, pero de todas maneras, a ver quién encuentra la solución: En una mesa hay tres sobres marcados con las letras A, B y C. Los tres contienen una cantidad (entera) diferente de euros y no hay ninguno vacÃo, con la peculiaridad …
Jun 04
Quiero presentar el trabajo que han publicado en Internet de la exposición “¿Por qué las matemáticas?â€?, concebida y realizada por iniciativa y con la colaboración de la UNESCO, por el Centre•Sciences (Centro de cultura cientÃfica, técnica de la región Centro – Orléans) y el Adecum (Asociación para el desarrollo de la cultura matemáticas – Orléans). …
Jun 02
Este acertijo lo leà en un libro de acertijos de Sam LLoyd. El acertijo de Sam Lloyd es más complicado que el que voy a enunciar yo, pero la forma de resolverlo es muy similar. A un joyero le dan cuatro trozos de cadena de tres eslabones cada uno, y le encargan que los una …
Jun 02
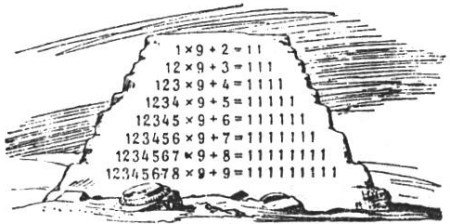
Este es el primero de una serie de acertijos y curiosidades matemáticas.Alguien es capaz de explicar por que se produce esta pirámide matemática: Se admiten todo tipo de explicaciones.
May 28
Os dejo un curioso GIF animado en el que tenéis que contar cuantos hombres hay. A ver quién encuentra la solución. Os recomiendo descargar la imagen y analizarla con el GIMP.
May 26
Aquà tenéis un sencillo juego de lógica para entreteneros. El objetivo es intercambiar las posiciones de las ranas. Las ranas sólo pueden saltar a la piedra de al lado si está libre o dar un salto por encima de otra rana. O sea, igual que en las damas. Nota(para bieito): basta recurrir a San google …
May 09
En el estupendo libro «El hombre anumérico» de John Allen Paulos, nos explica por que sabemos tan pocas matemáticas, por que somos analfabetos en matemáticas o lo que el llama anuméricos. En el libro, entre otras cosas trata de responder a las siguientes preguntas: ¿Es voluntaria esta resistencia que tenemos a entender los aspectos matemáticas …
