Este es el primer artículo que escribo en este nuevo dominio (aomatos.com). No tenía muy claro con que tipo de artículo escribir al comenzar esta nueva andadura. Tras mucho meditarlo, he decidido orientarme hacia esa pasión que siempre he tenido y sigue entreteniéndome tanto como las TIC: las matemáticas.
Alguna relación tenía que tener con las TIC,  la  web 2.0 y las redes sociales. Como no podía ser de otra forma y sumándome a la cresta de la ola, os hablo de twitter y de como nace este artículo.
Esta mañana leyendo mi timeline en twitter, me encuentro con una recomendación de un vídeo sobre números en la naturaleza de @koldo50 a @luismiglesias, @alaznez y un servidor.

@koldo50: Nature by Numbers http://t.co/8dXcZ6n vía @youtube cc/ @11110101 @luismiglesias @alaznez @aomatos

Lo primero que he hecho tras verlo, es guardarlo en Vodpod y pensar en este artículo.

Y ahora empieza la carga matemática, lo digo por si alguien quiere ir directamente al final y ver el vídeo.

Este excelente vídeo  de Cristóbal Vila nos habla de la presencia de los números y la geometría en la naturaleza con una secuencia de imágenes excepcional.
Más concretamente habla de la sucesión de Fibonacci y su presencia en la naturaleza.
La sucesión de Fibonacci es 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … , es decir se construye cada término sumando los dos números anteriores  partiendo del 0 y el 1 (en algunos sitios se habla de 1, 1, 2, 3,..). Esta sucesión, ya era conocida por los árabes y antes por los hindúes y fue publicada por primera vez por Leonardo de Pisa más conocido como Fibonacci en respuesta al famoso problema:

Una pareja de conejos tarda un mes en alcanzar la edad fértil. A partir de ese momento cada vez engendra una pareja de conejos, que a su vez, tras ser fértiles engendrarán cada mes una pareja de conejos. ¿Cuántos conejos habrá al cabo de un determinado número de meses?

El vídeo nos explica, de forma excelente, la construcción de la espiral de Fibonacci (una buena aproximación de la espiral logarítmica) que se consigue uniendo los vértices opuestos de los cuadrados que se forman siguiendo los números de la serie:

——->

Y partiendo de la espiral, lo enlaza con la concha del nautilus que no sigue una espiral de Fibonacci sino una espiral logarítmica pero como ya hemos comentado anteriormente,  la de Fibonacci  es una excelente aproximación.

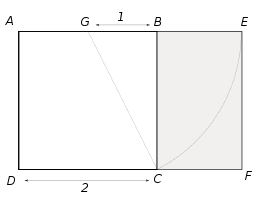
Luego, nos introduce el número áureo  φ(phi) de valor 1.61803399, tan conocido en las artes ya que describe la proporción áurea, que sorprendentemente está en la sucesión de Fibonacci como límite de la serie que surge al dividir un número entre su anterior: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8 …:

Vuelve con una de las más bellas presencias de la sucesión de Fibonacci: las espirales de Fibonacci en los girasoles con 21 espirales en el sentido horario y 34 en el otro (números de la sucesión):

Luego nos muestra el ángulo de oro que es ángulo resultante al dividir una circunferencia en dos ángulos de modo que el cociente entre ambos sea phi (el número áureo). El valor aproximado es 137,51º como se ve en el vídeo, para calcularlo basta con resolver una sencilla ecuación. Este es el ángulo que siguen las pipas del girasol en la construcción de las espirales.

Por último, acaba mostrándonos la propiedad de los hexágonos de pavimentar superficies como las alas de las libélulas y los ojos de los insectos. Con los hexágonos se consigue el máximo recubrimiento sin dejar espacios, con el mínimo material.

No os entretengo más, aquí tenéis el vídeo:

Comparte este artículo:!

•