Quiero presentar el trabajo que han publicado en Internet de la exposición “¿Por qué las matemáticas?�?, concebida y realizada por iniciativa y con la colaboración de la UNESCO, por el Centre•Sciences (Centro de cultura científica, técnica de la región Centro – Orléans) y el Adecum (Asociación para el desarrollo de la cultura matemáticas – Orléans). …
Categoría: Educación
May 09
La administración anumérica
En el estupendo libro «El hombre anumérico» de John Allen Paulos, nos explica por que sabemos tan pocas matemáticas, por que somos analfabetos en matemáticas o lo que el llama anuméricos. En el libro, entre otras cosas trata de responder a las siguientes preguntas: ¿Es voluntaria esta resistencia que tenemos a entender los aspectos matemáticas …
Mar 07
Vídeo de la evolución
He visto en «El blog de TIC» del IES Albalat de Navalmoral de la Mata, un extraordinario vídeo sobre la evolución en sólo 5′ 48». Aquí os lo dejo para que lo veáis: How Evolution Happens
Dic 18
Conferencia Jordi Adell
Durante este curso, si la matrícula lo permite, vamos a tener el lujo de contar como ponente en el curso «Nuevas tendencias en educación de la TIC» a Jordi Adell.Para aquellos que desconocen quién es Jordi Adell. Jordi Adell es Doctor en Filosofía y Ciencias de la Educación yprofesor del Departamento de Educación de la …
Dic 18
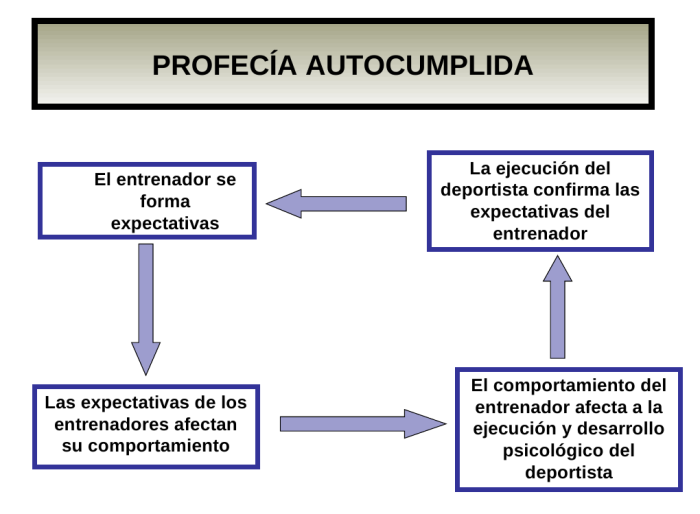
El efecto Pigmalion o la profecía autocumplida
En los cursillos de entrenadores de fútbol, en la signatura de psicología impartida por Javier Arana (excelente comunicador), nos han explicado el «Efecto Pigmalion» o la «profecía autocumplida». Para saber en que consiste os pongo la definición de la Wikipedia: El efecto pigmalión, llamado así en honor a Pigmalión -Rey legendario de Chipre y reputado …
May 26
¿Cómo aprendemos los humanos?
Leyendo diferentes blogs de mi interés, he encontrado en Cuaderno de aula esta perla del programa Redes que presentaba Eduard Punset. En esta entrevista de Eduard Punset a Roger Schank donde se habla de enseñanza y aprendizaje, podemos sacar interesantes conclusiones o por lo menos nos podría llamar a la reflexión de que cosas se …